In this research area, we designate the materials where non-trivial functional properties such as cross-correlated and nonreciprocal transport that arose from multiple degrees of freedom (multipole) appear as asymmetric quantum matters.
In planned research, we utilize a combination of advanced quantum beam, microfabrication technology, and high-resolution macroscopic measurements(A01), theoretical calculation and materials informatics(B01), and materials synthesis for typical and new materials (C01, C02) to explore new research on unveiling, design, and development. Our goal is to develop next-generation materials science that spreads to a wide range of research fields. We pursue the collaboration and merging of publicly offered research and planned research to develop novel material research fields. By maintaining the fundamental facilities for research, we support research activities in the area and support the next generation of researchers.
What are Asymmetric Quantum Matters?
Symmetry means the property of an object being invariant to a transformation. In solids, there are a variety of symmetries reflecting a periodic alignment of the atoms: spatial inversion, time-reversal, rotation, mirror, and translation symmetries. When some of the symmetries are lost owing to external fields and spontaneous phase transitions, the materials acquire functionalities; a ferromagnetic property appears when the time-reversal symmetry is lost, whereas a ferroelectric property appears when the spatial inversion symmetry is lost. Moreover, a multiferroic property, where the ferromagnetic (ferroelectric) property is controlled by an external electric (magnetic) field, can emerge when both spatial inversion and time-reversal symmetries are broken. By combining several symmetry breakings, infinite possible material properties are expected to open up. We refer to such materials hosting unconventional properties as “Asymmetric Quantum Matters”.
In this project, we try to explore unknown physical properties in Asymmetric Quantum Matters based on the concept of augmented multipoles. The augmented multipoles consist of four types of multipoles (electric, magnetic, magnetic toroidal, and electric toroidal) according to the space-time parities, which systematically describe any internal degrees of freedom in electrons, such as charge, spin, and orbital, as they provide a complete symmetry-adapted basis set in the low-energy Hilbert space. In other words, the augmented multipoles bridge a gap between microscopic electronic degrees of freedom and macroscopic symmetry, which is useful to understand/engineer/control physical properties in materials from a comprehensive viewpoint.
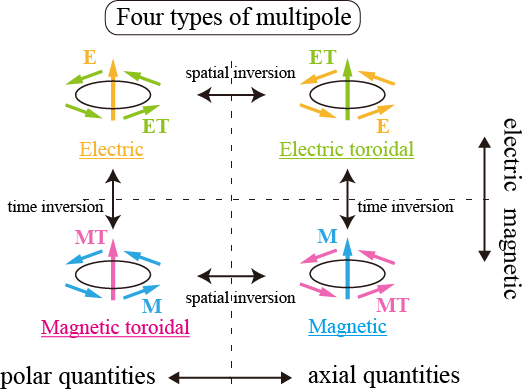
- S. Hayami and H. Kusunose, “Microscopic Description of Electric and Magnetic Toroidal Multipoles in Hybrid Orbitals”, J. Phys. Soc. Jpn. 87, 033709 (2018).
- S. Hayami, M. Yatsushiro, Y. Yanagi, and H. Kusunose,, “Classification of atomic-scale multipoles under crystallographic point groups and application to linear response tensors”, Phys. Rev. B 98, 165110 (2018)
- M. Yatsushiro, H. Kusunose, and S. Hayami,, “Multipole classification in 122 magnetic point groups for unified understanding of multiferroic responses and transport phenomena”, Phys. Rev. B 104, 054412 (2021)